hydraulics
All models are wrong but some are useful -George Box (Box 1976)
The study of modeling the flow of water over a surface is hydraulics. That particular topic (fluid dynamics), is a complex one that probes deep gaps in our collective knowledge of physical laws governing reality. the scale needed to represent the system to a degree of accuracy required, and the friction we experience as we carry assumptions and simplifications from conception to realization. As we make assumptions about the nature of nature, we can reasonably make simplifications to our system. In fluid sciences, one of the most powerful ones we can make is the inclusion or execution of particular forces, as the series of kinematic, diffusive, and dynamic wave model equations might exemplify, or in the reduction of the problems spatial dimensionality, as would be demonstrated by modeling the same domain using three-dimensional computational fluid dynamics solvers like TELEMAC-3D and one-dimensional hydraulic solvers like HEC-RAS 1D. These simplifications, sometimes referred to as “low complexity” models, are nearly universally favored over more the more complex representations of the world due to their conceptual and computational efficiency. While these low dimensional models have their uses, the real world is not as rigid and some knowledge is intrinsically lost in the simplification. This phenomenon is particularly present in the field of river hydraulics and open channel flow which was, and in may ways still is, dominated by one-dimensional models and measurement techniques. One of the assumptions made in these one-dimensional models is that all flow passes perpendicular through a given transect (cross section of a river). These 1-dimensional models have been used since the inception of computational fluid flow and have been widely adopted across public, private, and academic sectors. As an example, virtually all FEMA 100-year flood inundation maps are created using HEC-RAS 1D flow solver, a publicly available 1-dimensional flow solver from the U.S. Army Corp of Engineers.
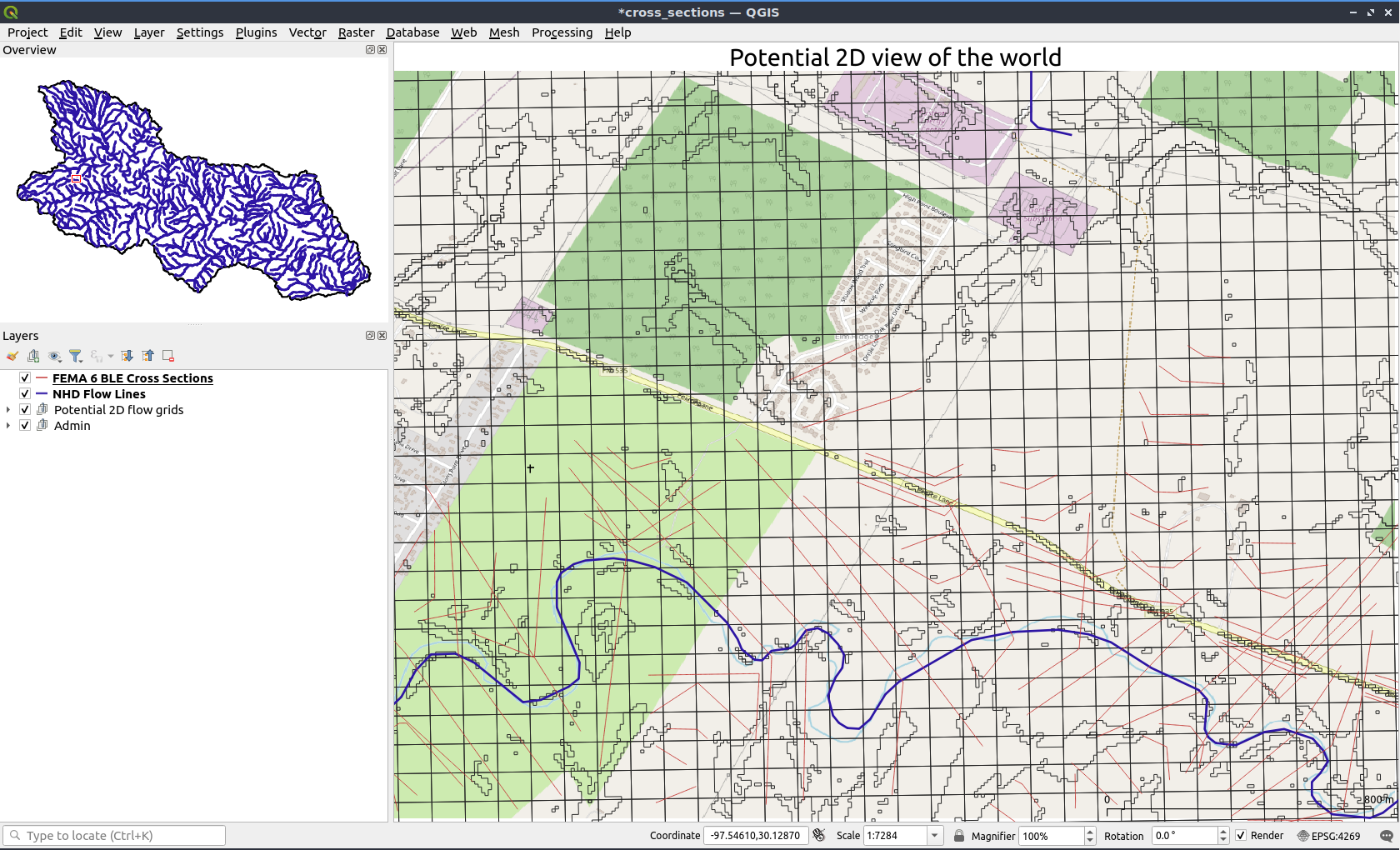
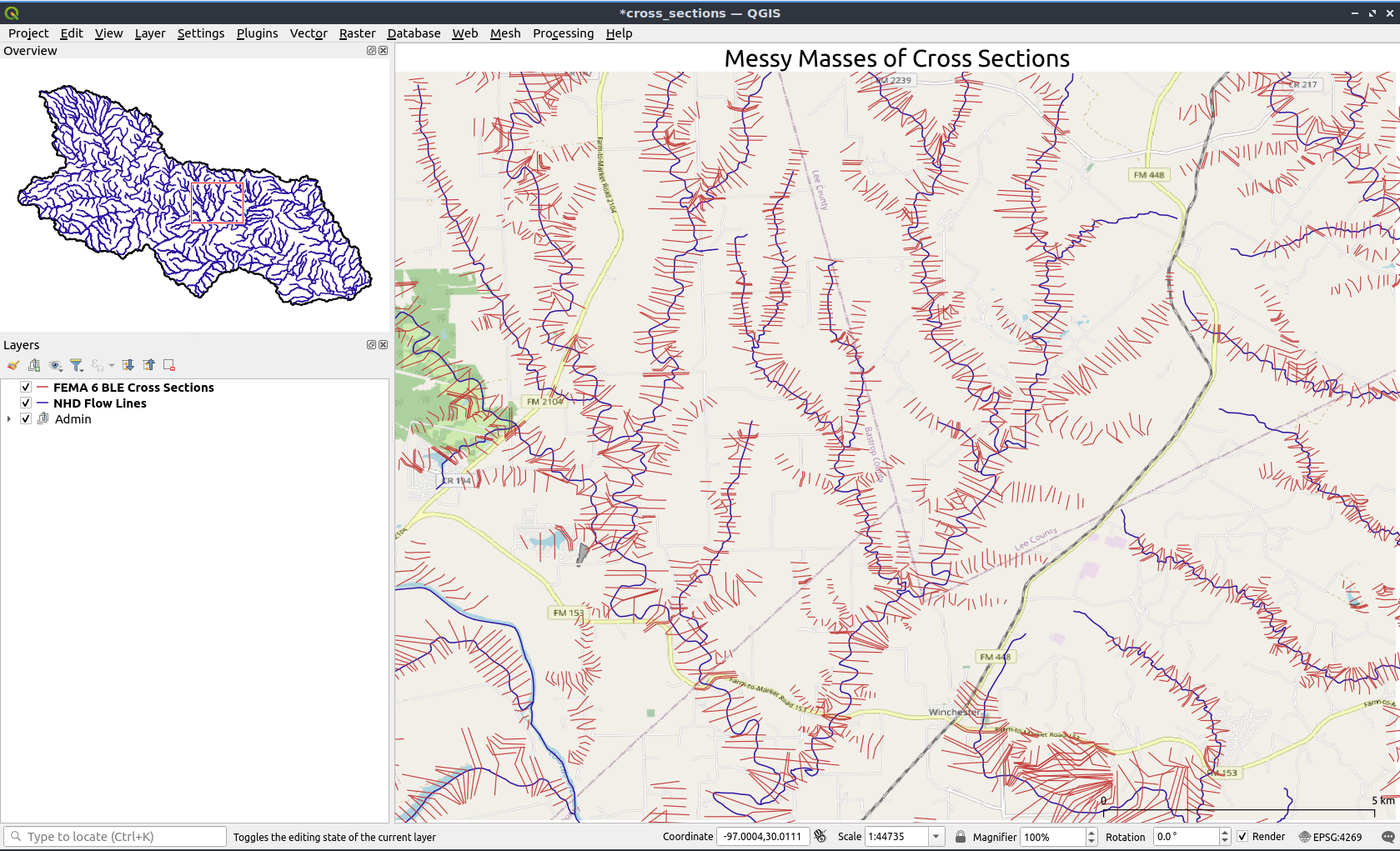
Although these 1-dimensional models have seen widespread acceptance and are used in scientific, engineering design, and operational capacities, they require extensive knowledge and judicious use of modeler discretion in order to provide serviceable results. It is also not uncommon to find that model results that may be realistic in one transect, may be off by several feet in another. Post-event analysis of such failures universally point to mis-parameterization of the model or a violation of the models assumptions. Additionally, this type of modeling, while widely applicable to a single reach, is wholly unsuited to widespread applications in flooding. As seen in Figure 1, when the application in question requires the inclusion of more than one reach, the workflow and system that is needed to appropriately addresses the complexities of that merger grows exponentially.
Given that and the state of advancement computers continue to experience, it seems rather a rather aimless exercise to devise and execute a convoluted series of steps to couple model. At that level of complexity, is it not simply better to increase the dimensionality of the problem and present a clearer path towards explainability, potential gains in accuracy, at the “cost” of computation time?